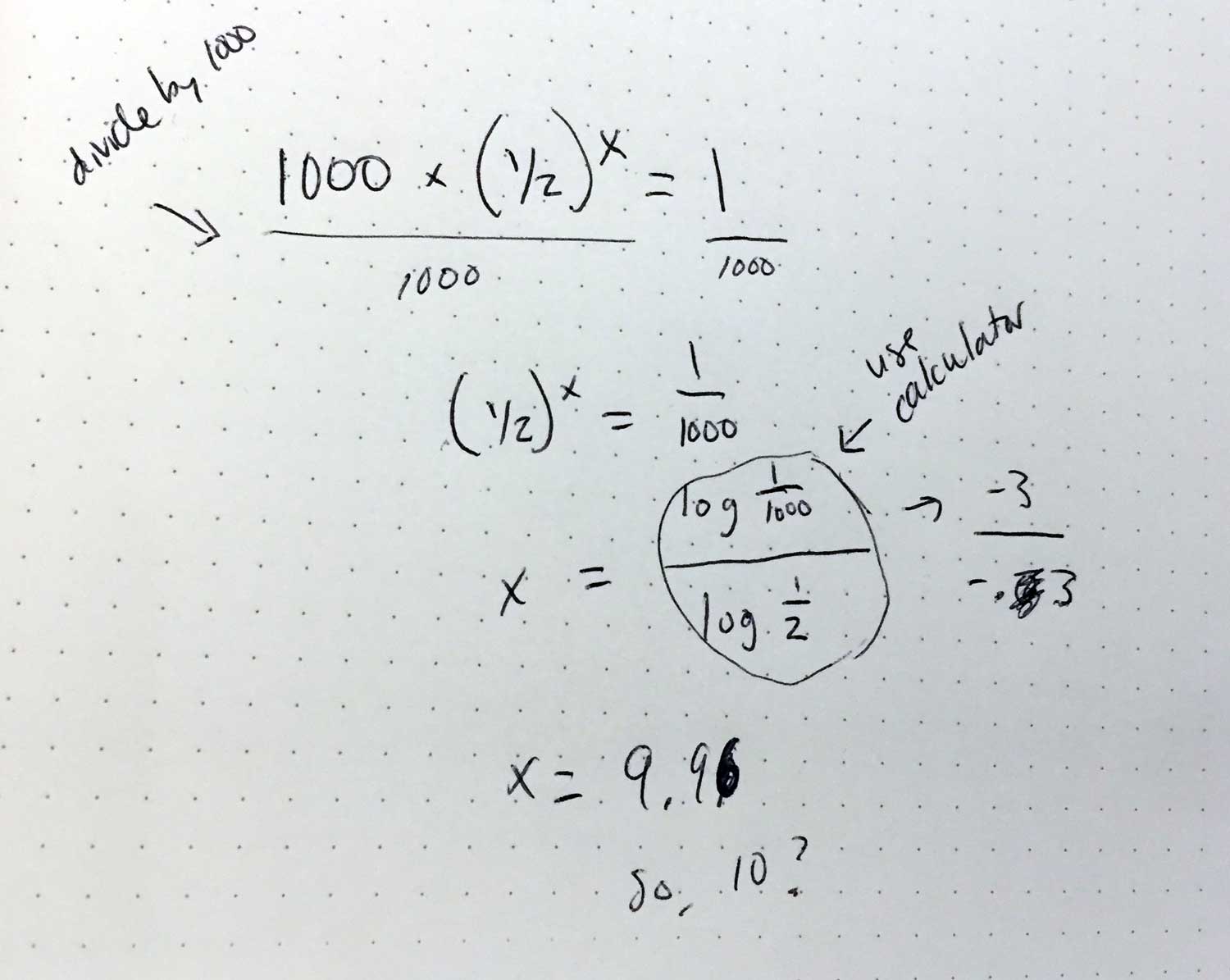If I told my 16-year-old, art student self I’d be writing a blog post about this, I wouldn’t have believed it. Yet, here I am, not only learning about this stuff but also understanding it!
Before delving into logathrims and Big-O, I had a fundamental understanding of binary search. These two resources made it click for me:
See the Pen Linear vs Binary Search by Ron Gierlach (@youfoundron) on CodePen.
After that, I kept running into mention of Big-O here and began to understand it as a way to express an algorithm’s efficiency, which it is! Vaidehi Joshi’s explanation on BaseCS made the concept behind Big-O click for me.
Big-O Notation
Here’s how I understand it:
Big-O notation is a way to mathematically express how an algorithm performs as its input increases. Here are a few common expressions:
- Constant or
O(1). This one is the fastest; the time it takes for the algorithm to execute doesn’t change depending on the size of your data (accessing something on top of a stack, for example). - Logarithmic or
O(log n). Fast and scales well with more input (binary search). - Linear or
O(n). The algorithm execution time slows down proportionally to the amount of input. - Quadratic or
O(n²)or bad news bears. This algorithm gets exponentially slower as its input grows. I don’t know of a specific algorithm at the moment, but I would equate this to how quickly people become too drunk if they booze on an empty stomach.
Here’s a cool chart that shows the above information on a graph:

Big-O notation is used to describe space and time complexity.
This post on Stack Overflow was super helpful in learning about this stuff. From my understanding:
Space complexity refers to any space or memory increases required by an algorithm and how they increase with more input. For example, you may use a temporary variable to compare two items in a sorting algorithm – this temporary variable constitutes an increase in space used. If you find that you need to add a new temporary variable for each new item in the input, that would be a bad Big-O expression like O(n²) or the worst, O(n!), but if you only need one temporary variable, no matter the input size, then that would be linear space, or O(1), I think.
Time complexity refers to how much longer an algorithm takes to execute as input increases. Array sorting algorithms, for example, generally have pretty bad time complexity since the more elements there are, the longer it will take to complete the sort. Binary search, however, has pretty great time complexity since a number of elements being searched impacts the time logarithmically.
Okay, on to logarithms!
Logarithms
Until writing this post, I had a small panic attack every time I ran into the mention of logarithms in my data structures studies. Once again though, Vaidehi to the rescue in BaseCS! I highly recommend sitting quietly for 15 minutes and thoroughly reading Looking For The Logic Behind Logarithms. I am constantly amazed at how well she writes and makes these seemingly complicated concepts understandable with drawings and notes. In this section, I will pretty much summarize what she says based on my understanding.
Something I came up with that helps me understand: A logarithm is the opposite of an exponent in the same way subtracting is the opposite of adding, and dividing is the opposite of multiplying. That is very basic and probably obvious for some, but not for others (me).
Binary search is an algorithm that is in logarithmic time, so it’s a great one to use. In other words, the number of times binary search runs increases logarithmically with the number of elements it has to search. This is the opposite of an exponential increase. For example, the algorithm must run a maximum of 2 times to search 4 items, 3 times to search 8 items, and only 5 times to search 32 items. Considering 32 is 8 times more elements than 4, and only requires 3 more runs, that’s pretty good. How many runs would be for 1000 items?
Let’s see if I can actually do some math. Breaking it down:
16 x (1/2)⁴ = 1(Binary search must break 16 in half four times to have 1 result remaining)n x (1/2)ˣ = 1(n = number of items to search, x = times needed to break in half to reach result)1000 x (1/2)ˣ = 1(Now I will Google, “how to solve for x if its an exponent”)
I was expecting something equivalent to “divide each side by 1000 then remove then do something to isolate the x” and, remarkably, I was correct. According to this video, we then have to…use a calculator! I can confidently say this is the first time since high school that I have used a calculator for something other than add/subtract or multiply/divide.
So, in the spirit of BaseCS, here is a visualization on graph paper:

According to my very advanced algebraic calculations, binary search would need to run 10 times for 1000 items. Let’s see if that’s correct…
Yes, I just Googled “how many times would binary search have to run for 1000 items” because, why not? And someone else had the exact same question because this is the Internet, after all!
And guess what? I’m right! I JUST DID MATH! With that, I am going to wrap up this post because I am so damn proud of myself.
Back to binary search for a sec. The algorithm only had to run another 5 times to search 968 more items which is pretty darn efficient! Binary search for the win. Now I am going to draw a conclusion connecting binary search to hash tables:
Binary search can only search numbers, not words or letters. What does a hash function do? It turns letters into numbers! So, I think binary search and hash tables are probably great friends. I’m starting to see the dots connect here and, although I am not sure how all of this will relate back to WordPress and my day-to-day, I am confident it will somehow!
In JavaScript
Drum roll please…
Here is an implementation of binary search in JavaScript! I pretty much followed the pseudocode guides in the Khan Academy lesson – I suggest you do the same! I crashed CodePen a lot but ultimately figured it out.
See the Pen Binary Search by Lara Schenck (@laras126) on CodePen.
What’s next?
A beer! Actually no, more like a short break to walk to the library then sorting algorithms and/or tree search algorithms. Stay tuned!